British flag theorem

Hace unos días propusimos este reto geométrico. Lo podemos plantear como un caso particular del Teorema de la Bandera Británica. Este teorema afirma lo siguiente:

Si \(P\) es un punto interior a un rectángulo \(ABCD\), entonces la suma de los cuadrados de las distancias de \(P\) a dos vértices opuestos es igual a la suma de los cuadrados de las distancias de \(P\) a los otros dos vértices. Es decir, \(\overline{AP}^2+\overline{CP}^2=\overline{BP}^2+\overline{DP}^2\).

British flag theorem

Esta propiedad es una aplicación directa del Teorema de Pitágoras y dejamos su demostración como ejercicio.

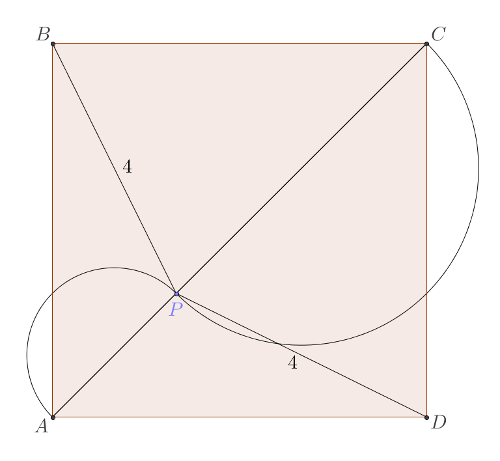
En cuanto al reto, si \(P\) es el punto en la diagonal \(AC\) del que parten ambas semicircunferencias (ver imagen superior de la entrada), por el teorema de la bandera británica se tiene que \(\overline{AP}^2+\overline{CP}^2=4^2+4^2=32\).

Por otro lado, la suma de las áreas de ambos semicírculos es \(\frac{\pi}{2} (\frac{\overline{AP}}{2})^2+\frac{\pi}{2}(\frac{\overline{CP}}{2})^2=\frac{\pi}{8}(\overline{AP}^2+\overline{CP}^2)=4\pi\).

Conocí el Teorema de la bandera británica gracias @elderiofer