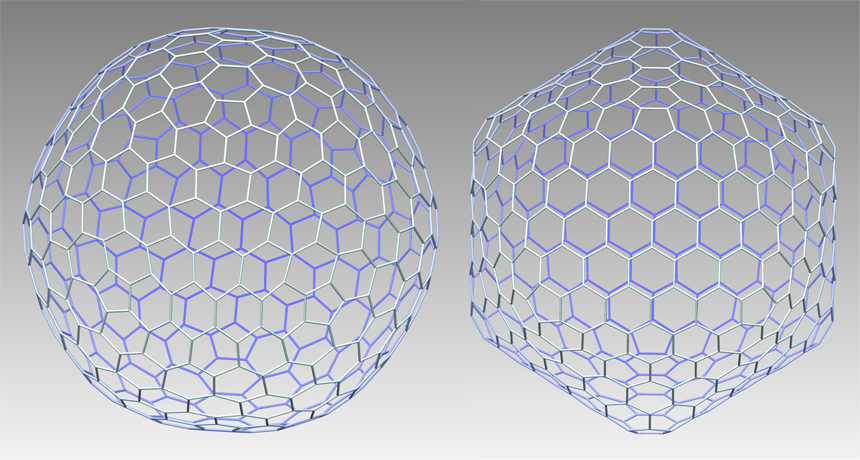
 Recientemente los investigadores Stan Schein y James Maurice Gayed, de la Universidad de California Los Ángeles, parecen haber descubierto la existencia de un nuevo tipo de sólido geométrico. Schein y Gayed se han inspirado en el trabajo de Michael Goldberg, quien describió en 1937 un conjunto de cuerpos geométricos que se conocieron como poliedros de Goldberg, pese a que en realidad no eran poliedros ya que no tenían su caras planas (tenían ángulos internos). Los investigadores Schein y Gayed afirman haber encontrado una forma de conseguir que estos ángulos internos sean cero, lo cual implica que las caras son planas y se trata de verdaderos poliedros (aunque en el proceso las caras hexagonales dejan de ser regulares). Schein encontró estas formas estudiando una proteína llamada Clatrina, esta vez con caras planas. En honor al trabajo de Goldberg, han decidido llamar a estos nuevos sólidos, “poliedros de Goldberg”.
Recientemente los investigadores Stan Schein y James Maurice Gayed, de la Universidad de California Los Ángeles, parecen haber descubierto la existencia de un nuevo tipo de sólido geométrico. Schein y Gayed se han inspirado en el trabajo de Michael Goldberg, quien describió en 1937 un conjunto de cuerpos geométricos que se conocieron como poliedros de Goldberg, pese a que en realidad no eran poliedros ya que no tenían su caras planas (tenían ángulos internos). Los investigadores Schein y Gayed afirman haber encontrado una forma de conseguir que estos ángulos internos sean cero, lo cual implica que las caras son planas y se trata de verdaderos poliedros (aunque en el proceso las caras hexagonales dejan de ser regulares). Schein encontró estas formas estudiando una proteína llamada Clatrina, esta vez con caras planas. En honor al trabajo de Goldberg, han decidido llamar a estos nuevos sólidos, “poliedros de Goldberg”.
Este nuevo tipo de poliedros podría tener diversas aplicaciones, desde mejorar la aerodinámica de una pelota de golf hasta el desarrollo de nuevos fármacos —algunos virus, como el de la gripe, tienen una forma similar al poliedro de Goldberg.
Pueden encontrar en ScienceNews más información.
S. Schein and J.M. Gayed. Fourth class of convex equilateral polyhedron with polyhedral symmetry related to fullerenes and viruses. Proceedings of the National Academy of Sciences. Published online February 10, 2014. doi: 10.1073/pnas.1310939111.

