Visto en Francis (th)E mule Science's News
Las bandadas de estorninos (Sturnus vulgaris) se caracterizan por una curiosa propiedad: cada estornino ajusta su movimiento en función del de los siete vecinos que le rodean. Este número es independiente del número de individuos y de su densidad. El misterio tiene una explicación: el equilibrio entre la cohesión del grupo y el esfuerzo individual, cuando hay incertidumbre en la detección de la posición de los vecinos, tiene un coste sensorial y cognitivo mínimo cuando la interacción mutua se reduce a entre seis y siete vecinos. Esta solución se ha obtenido estudiando la bandada como un sistema dinámico lineal (sistema de ecuaciones diferenciales ordinarias) con ruido en la interacción entre individuos. Cada pájaro en la bandada responde a un número fijo de vecinos (m) y cada interacción tiene un cierto coste (esfuerzo) proporcional a la distancia de separació. Como la bandada tiene que responder a las señales externas del entorno (vigilar y evitar depredadores, buscar comida, sitios de descanso, etc.), lo más razonable es que el esfuerzo que cada individuo necesite para mantenerse en la bandada sea el mínimo posible. Aunque el modelo utilizado es muy sencillo, los autores han utilizado simulaciones por ordenador para determinar el número óptimo de vecinos (m*) que minimiza el coste y el efecto negativo del ruido en la interacción. El resultado, que no depende del número de individuos, es un número entre seis y siete, aunque para bandadas muy planas el valor crece hasta 10. L0s autores del estudio afirman que sus conclusiones son aplicables a bancos de peces, enjambres de insectos, rebaños de animales y otras agrupaciones similares de animales. El artículo técnico es Young GF, Scardovi L, Cavagna A, Giardina I, Leonard NE, “Starling Flock Networks Manage Uncertainty in Consensus at Low Cost,” PLoS Comput. Biol. 9: e1002894, 2013.
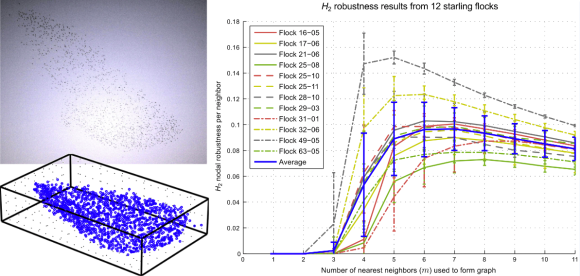
El modelo matemático utilizado por los autores es lineal, aunque la presencia de ruido impide una solución analítica. El coste la interacción entre dos estorninos se ha supuesto constante, agrupando la demanda energética sensorial y neurológica necesaria para observar el comportamiento del vecino, así como buscar depredadores, comida, etc. Por ello, el coste global de la interacción con m vecinos crece linealmente con dicho número. La componente de ruido en la interacción hace que cada estornino siga un camino aleatorio. El estado global del sistema corresponde al movimiento conjunto de la bandada. Para valores pequeños de m, la bandada es poco robusta y los individuos acaban disgregándose. Para valores grandes de m, el coste de las interacciones es muy elevado. Como resultado, se espera la existencia de un valor óptimo m* intermedio. Los resultados de las simulaciones muestran que el valor óptimo m* crece muy débilmente con el tamaño del grupo (la pendiente de un ajuste lineal es 0,018) y con el incremento de la robustez (la pendiente de un ajuste lineal es 0,023), lo que permite afirmar que en la práctica es constante.
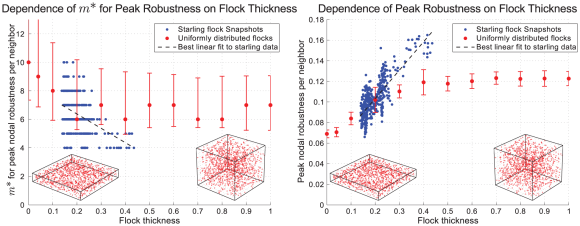
La forma de la manada se estima mediante el momento de inercia, es decir, se aproxima por un elipsoide que tenga como ejes sus ejes principales de inercia. El valor óptimo m* y el valor de la robustez pico dependen del factor de aspecto de la manada, definido como el cociente entre el diámetro más pequeño y el más grande del elipsoide. Los estudios experimentales indican que las bandadas de estorninos tienen un factor de aspecto entre 0,13 y 0,44, la mayoría entre 0,13 y 0,27. Para estos factores de aspecto, el valor óptimo m* se encuentra entre 6 y 7. Para bandadas más planas (como rebaños de animales terrestres), con factores de aspecto menores de 0,1, el valor óptimo m* se aproxima a 10. Para bandadas más esféricas , con factores de aspecto cercanos a la unidad, el valor óptimo es 7.
La próxima vez que veas una bandada de estorninos piensa que su comportamiento colectivo emerge de interacciones locales entre más o menos siete individuos. Si no vives en el campo, hay muchas fotos en la web (fotos y vídeos).