Bueno, parece que las fiestas navideñas no han sido muy propicias para resolver problemas, porque aunque algunos nos han asegurado que el problema 1 lo han conseguido resolver fácilmente, nadie ha perseverado lo suficiente para resolver el Problema 2. Tendremos que dejar el premio desierto esta vez, y pensarnos si ponemos un premio en metálico (¿un tornillo tal vez?) para la próxima.
Para los que tienen curiosidad por saber la solución, ahí va. Se admiten comentarios de ánimo a los sufridos pensadores de problemas. Snif.
El enunciado era el siguiente:
Supongamos que hay nueve amigos en un restaurante chino sentados en una mesa circular. Cada uno pide un plato diferente que el camarero va depositando en el centro de la mesa, en la típica plataforma giratoria que permite compartir los diferentes platos.
Problema 1 (fácil):
Supongamos que el camarero ha dispuesto los platos, cada uno frente a un comensal, de forma que ninguno de ellos cae frente al que lo había pedido. Demuéstrese que, girando la plataforma, es posible conseguir que al menos dos platos se sitúen frente a quien los encargó.
Problema 2 (no tan fácil):
Supongamos que el camarero ha dispuesto los platos de forma que exactamente dos de ellos caen frente a los que lo habían pedido. Demuéstrese que, girando la plataforma, existe otra posición distinta en la que también hay al menos dos platos que se sitúan frente a quien los encargó.
Solución:
Problema 1: Este problema se resuelve fácilmente con el conocido principio del palomar. Sabemos que la mesa tiene 9 posibles posiciones. A cada comensal le corresponde una posición de la mesa (la que le deja el plato delante) que no puede ser la posición dispuesta por el camarero. Por tanto hay 9 comensales para 8 posiciones, así que es imposible que a todos los comensales les correspondan posiciones distintas. Es decir, habrá alguna posición de la mesa que deje al menos dos platos frente a quien los encargó.
Problema 2: Vamos a numerar a los comensales (o a sus posiciones en la mesa) con los números del 0 al 8, de manera que los que tienen sus platos delante en la disposición original son el 0 y el \(i\).
La disposición de los platos es una permutación de estos 9 números \(\pi(0),\pi(1),\ldots,\pi(8)\), donde sabemos que \(\pi(0)=0\), que \(\pi(i)=i\) y que \(\pi(j)\neq j\) para todo \(j\neq i,0\). Observemos que, dado un comensal \(j\), el número de posiciones que hay que girar la mesa para que tenga el plato delante es \(\pi(j)-j \) (mod 9).
Veamos una propiedad interesante: la suma de todos los números \(\pi(j)-j\) es igual a 0, porque esta suma es igual a
\((\pi(0)+\pi(1)+\cdots+\pi(8)) -(0+1+\cdots +8) = (0+1+\cdots + 8)- (0+1+\cdots +8) = 0\).
Por tanto esta suma también es obviamente 0 (módulo 9).
Si los números \(\pi(j)-j\) con \(j\neq i,0\) fueran todos distintos (módulo 9), esto querría decir que hay 7 números distintos, entre 1 y 8, cuya suma es igual a 0 (módulo 9). Pero por otro lado los números del 1 al 8 suman 36, que es 0 (mod 9). Por tanto, si los 7 números citados fueran distintos, el número que falta sería 36 menos la suma de todos ellos, luego también sería 0 (módulo 9), lo cual es imposible. Por tanto, hay al menos dos números de la forma \(\pi(j)-j\) que son iguales (módulo 9) y no nulos. Girando la mesa precisamente ese número de posiciones, habrá al menos dos comensales con sus platos delante.
Curiosidad: ¡El enunciado del problema 2 sólo es válido si el número de comensales es impar! En efecto, hemos usado que la suma de los números del 1 al 8 es 0 (mod 9). Si tuviéramos \(n\) comensales, la suma de los números del 1 al \(n-1\) sería \(n(n-1)/2\), que es múltiplo de \(n\) si y sólo si \(n\) es impar (y por lo tanto \(n-1\) es par).
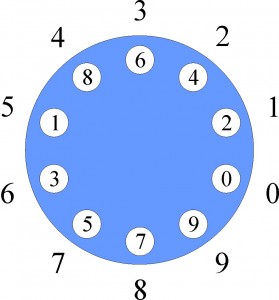
De hecho, para un número par (\(2k\)) de comensales, se pueden distribuir los platos de la forma: \(0,2,4,\ldots,2k-2,1,3,5,\ldots,2k-3,2k-1\), y los números \(\pi(j)-j\) (mod \(2k\)) serían \(0,1,2,\ldots,k-1,k+1,k+2,\ldots,2k-1,0\), siendo esta la única posición en que dos comensales (y no más) tienen sus platos delante. En la figura puede verse este ejemplo con 10 comensales, por si alguno quiere imprimirlo, recortarlo y comprobarlo, girando el círculo y acordándose al mismo tiempo de los teléfonos de su infancia.
