Hemos recibido dos soluciones válidas al problema, aportadas por nuestros queridos lectores Ramón Piedra y Alberto Castaño.
Recordemos el enunciado del problema:
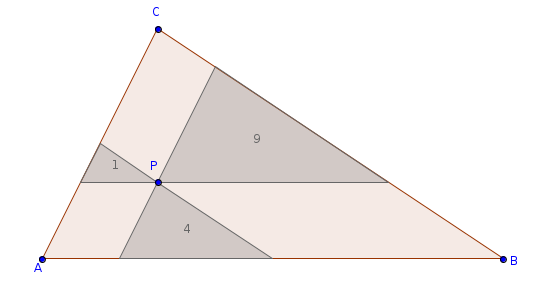Consideremos un punto \(P\) interior a un triángulo de vértices \(A\), \(B\) y \(C\). Si trazamos desde \(P\) tres rectas paralelas a cada uno de los lados, se forman los tres triángulos interiores que se ven en la figura.
Si las áreas de los triángulos interiores son 1, 4 y 9 ¿cuál es el área del triángulo de vértices \(A\), \(B\) y \(C\).?
En general, si las áreas de los triángulos pequeños son \(S_1\), \(S_2\) y \(S_3\) ¿es posible dar una fórmula para el cálculo del área del triángulo grande?
Como bien dice Alberto, la solución afirmativa al problema general nos aporta la solución al primer problema. La solución que él aporta se basa en semejanza de triángulos. Dos triángulos se dicen semejantes si tienen los mismos ángulos y, en consecuencia por el teorema de Thales, sus lados son proporcionales.
Es evidente que en este caso, dado que las rectas trazadas desde \(P\) son paralelas a los lados, los tres triángulos pequeños son semejantes entre sí y semejantes al triángulo grande.
Dados dos triángulos semejantes \(T\) y \(T’\) tales que los lados de \(T\) son \(\lambda\) veces los de \(T’\), se deduce fácilmente que el área de \(T\) es \(\lambda^2\) la de \(T’\). Transcribimos desde aquí la solución dada por Alberto, que es muy parecida a la que habíamos pensado nosotros:
Por ser los triángulos semejantes, existirán tres constantes \(\lambda_1\), \(\lambda_2\) y \(\lambda_3\) tales que
\(S_1 = \lambda_1^2S\), \(S_2 = \lambda_2^2 S\) y \(S_3 = \lambda_3^2 S\).
Es más, si, respectivamente, llamamos \(Q\) y \(R\) al corte de la recta paralela a \(AB\) que pasa por \(P\) con los lados \(AC\) y \(BC\) y \(X\) e \(Y\) a los cortes del lado \(AB\) con las rectas paralelas a \(AC\) y \(BC\) pasando por \(P\) , también tendremos que
\(QP =\lambda_1 AB,\ PR = \lambda_2 AB\mbox{ y }XY = \lambda_3 AB\).
Ahora bien, por ser \(AXPQ\) e \(YBRP\) dos paralelogramos, \(AX = QP\) e \(YB = PR\), con lo que \(QP + XY + P R = AB\). Reuniendo todo lo anterior, obtenemos el siguiente sistema de ecuaciones:
\(\left\{\begin{array}{l} S_1 = \lambda_1^2 S\\ S_2 = \lambda_2^2 S\\ S_3 = \lambda_3^2 S\\\lambda_1+\lambda_2+\lambda_3 =1.\end{array}\right.\)
Este sistema tiene como única solución
\(\displaystyle \lambda_1=\frac{\sqrt{S_1}}{\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3}},\ \lambda_2=\frac{\sqrt{S_2}}{\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3}}\mbox{ y }\lambda_3=\frac{\sqrt{S_3}}{\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3}}\).
Y por lo tanto
\(S=(\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3})^2\)
En el contexto de la primera pregunta,
\(S = (1 + 2 + 3)^2 = 36\).
La solución que aporta Ramón es esencialmente la misma, aunque planteada a partir de las coordenadas baricéntricas de \(P\). Dados tres puntos no alineados \(A\), \(B\) y \(C\), se dice que las coordenadas baricéntricas de \(P\) son \((t_1,t_2,t_3)\) si
\(\overrightarrow{AP}=t_1\overrightarrow{AB}+ t_2\overrightarrow{AC}\) y \(t_1+t_2+t_3=1\).
A partir de aquí se prueba que la relación entre las áreas es justamente \(S_1=t_1^2S,\ S_2=t_2^2S\mbox{ y }S_3=t_3^2S\), que junto con \(t_1+t_2+t_3=1\) nos da el mismo sistema que resuelve Alberto.
