De Mari Carmen Díez Navarro en INFORMACIÓN
Este curso, y casi desde el principio, he podido observar que mis alumnos están muy interesados por los números y por contar. Son actividades que desde el primer día he promovido, por pedagogía y por costumbre, y a las que los niños están respondiendo con énfasis y afición.
Habitualmente contamos cuántos niños hay en cada mesa, cuántos hay «en total», si hay empates o no. También contamos los pisos de las torres de madera que construyen, las albóndigas del guisado, los que son de un equipo de fútbol o de otro, los que llevan gafas, los que tienen el pelo rizado o liso, las personas que hay en cada casa, los dientes que se les van cayendo?
La verdad es que lo contamos todo, porque con el tiempo y la formación he concluido que trabajar con los números en la escuela infantil pasa por invitar a los niños a mirar la vida con ojos matemáticos. Así los números se viven como un juego y se aprende a comparar, relacionar, ordenar, clasificar y contar como las actividades vitales, útiles y entretenidas que realmente son. Así los números se palpan, se sienten, se perciben como importantes, se cargan de afecto.
A los niños les interesa saber sus años y los de sus padres, su peso, su medida, su talla de camiseta y de zapatos, los días que faltan para ir de excursión o celebrar una fiesta? Les suele atraer medir, pesar, manipular, hacer colecciones, grupos, escaleras de tamaños, discriminar las formas o los colores, contar, conocer «los números largos», averiguar «si el cero tiene algo dentro», etc. El caso es contar con sentido, lo que viene a ser: entender, poner orden e ir dominando el mundo a su alcance.
En estos aconteceres matemáticos a mí me gusta ver a Nico presumiendo de que sabe sumar y demostrándolo al contar los dedos que él mismo se prepara en un reto constante, a Héctor que se ha dado cuenta de que es el único que lleva una camiseta de la talla 8, a Celia que recita «la tabla del 1» que se la ha enseñado su hermana, a Aitana que se pregunta cómo es que su bebé tiene «cero años» si el cero no es «nada» y hace ya muchos días que la nena vive en su casa…
El otro día escuché a varios niños enzarzados en una divertida conversación sobre las edades de sus padres:
-Mi mamá nació un año antes que mi papá.
-Pues mi padre es más mayor que mi madre.
-Mis padres empatan a 42.
-Mi papá tiene 58, es el que más años tiene de todos los de aquí.
-Mi mamá gana a todos también, es la que más pocos tiene: 31.
-Por eso está tan guapa.
-Oye, que mi padre también es guapo, aunque tenga 58.
Otro día Martina contó: «El domingo hice una ruta que tenía 1.000 escalones». Valoré su hazaña y escribí el número 1.000 en la pizarra, insistiendo en que era una buena deportista. Pero por lo visto mi entusiasmo despertó la rivalidad de uno de sus compañeros.
-El cero no es nada y el 1 es poco, así es que no será tanto el 1.000.
-Sí que es, que yo me cansé bastante, contestó Martina, dándose por aludida.
-Pues yo al 1.000 lo veo poquísimo, insistía él.
-Mi yayo me da 5 euros a veces y me compro muchas cosas, comentó una niña.
-A mí me encantan los números largos, porque me gusta tener mucho de todo.
-Bueno, pero el 1.000 no es tanto, repetía el inconforme.
Ante esta empecinada rebelión celosa, intuí que ningún argumento sería lo suficientemente bueno, así que opté por poner un ejemplo para que al menos a los demás niños les quedara un poco más claro el tema, y a él lo dejé que rumiara su rabieta. Ya se sabe que los sentimientos a veces nos hacen perder el norte.
De una manera o de otra la discusión ha sido útil. Por un lado, para que los niños vayan acercándose a estas matemáticas de a pie que manejamos en la escuela infantil y por otro para que salgan a relucir ciertos sentimientos que conviene aprender a reconocer, expresar y encarar adecuadamente para que no se transformen en agresiones o en silencios explosivos. Virtudes de las matemáticas aplicadas y de la libre expresión que gastamos por aquí.
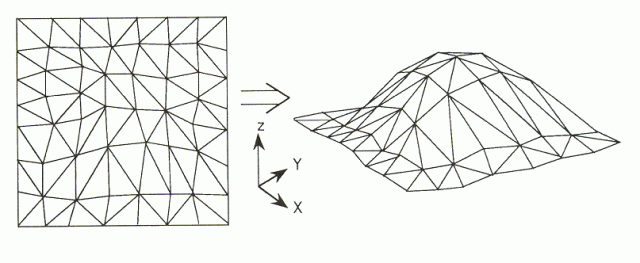Hoy queremos compartir con vosotros la entrada titulada Me gustan los triángulos, escrita por Clara Grima para Naukas.
