Os enlazamos aquí una página con casi 1600 vídeos sobre matemáticas, muy interesante… y abundante.
Vídeos, vídeos y más vídeos
Categoría: Matemáticos
Aprenda un poco de lengua francesa con… California Dreaming
Cierto… el título de esta entrada parece un poco discordante ¿no debería ser Aprenda un poco de Inglés con… California Dreaming?
Pero es el título que Cédric Villani ha escogido para esta entrada en su blog, en la que habla de su actual estancia en el Mathematical Sciences Research Institute (MSRI) de Berkeley, en California.
Continuar leyendo en el blog de Cédric Villani.
El teorema de Zeckendorf o “Magia y Fibonacci”
De lo que hablamos hoy aquí ya se habló en Divulgamat y ZTFNews.org, y también en Gaussianos.
Edouard Zeckendorf fue un médico, oficial del ejercito y matemático belga que, en 1972, publicó el siguiente teorema:
Todo número entero positivo puede representarse de forma única como suma de números de Fibonacci (esto es, elementos de la sucesión de Fibonacci) distintos, de tal forma que dicha representación no contiene dos números de Fibonacci consecutivos.
Esta representación se denomina representación de Zeckendorf del número entero positivo en cuestión.
La demostración de la existencia se realiza por inducción. Dicho muy esquemáticamente, se supone el resultado cierto para cualquier entero positivo menor que uno dado \(N\), se escoge el mayor número de Fibonacci \(F_j\) menor o igual que \(N\) y se aplica la inducción al número \(N-F_j\).
Así, para obtener la representación de Zeckendorf de \(1954\), escogemos el mayor número de la sucesión que sea menor o igual que \(1954\), ya saben, \(1597\). La diferencia es \(1954-1597=357\). Ahora el número de Fibonacci más cercano a \(357\) es \(233\). Restando \(357-233=124\). Escogemos \(89\) como el siguiente número de Fibonacci en la representación de Zeckendorf, \(124-89=35\). Como \(34\) está en la sucesión de Fibonacci, la representación es:
\(1954=1597+233+89+34+1\).
(Por supuesto, para la representación de Zeckendorf no contamos el $atex 0$ y sólo tomamos uno de los dos términos iguales a \(1\))
La unicidad se basa en el siguiente lema:
La suma de cualquier conjunto no vacío de números de Fibonacci, no consecutivos, cuyo mayor elemento sea \(F_j\), es estrictamente menor que el siguiente término \(F_{j+1}\).
Una aplicación curiosa de esta representación es el paso de millas a kilómetros y viceversa. Dado que la razón aúrea es
\(\displaystyle\varphi\approx 1’6181033\ldots =\lim_{n\to\infty}\frac{F_n}{F_{n+1}}\),
muy parecida a la razón entre millas y kilómetros: \(1’6093\), para pasar (aproximadamente) \(N\) millas a kilómetros se puede sustituir cada término en la representación de Zckendorf de \(N\) por su siguiente en la sucesión de Fibonacci. Es decir
\(1954=1597+233+89+34+1\) millas
son aproximadamente
\(3162=2584+377+144+55+2\) kilómetros.
Otra aplicación del teorema es el siguiente juego, que consiste en adivinar cualquier número que el auditorio haya pensado entre \(1\) y \(100\). Para ello, una vez que se han puesto de acuerdo, a tus espaldas, en escoger un número, tú les vas presentando una por una estas 10 tarjetas con números “aleatorios”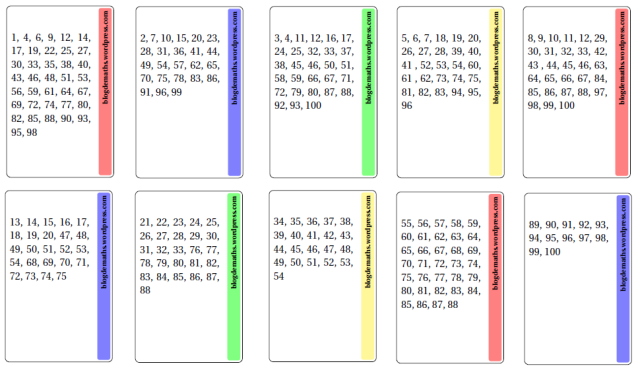
y ellos tienen que decir si su número se encuentra en ellas o no. Astútamente estas tarjetas las hemos fabricado de tal forma que comienzan por un número de Fibonacci, que está seguido por todos aquellos, mayores que él, que lo contienen en su representación de Zeckendorf.
Por ejemplo, si el número que han pensado es \(32\) escogerán las siguientes tarjetas 
y nosotros sólo tendremos que sumar los primeros números de cada tarjeta,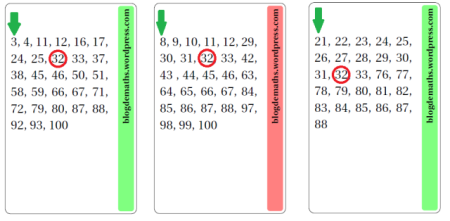 
pues la representación de Zeckendorf de \(32\) es \(32=21+8+3\).
El juego admite una variante que lo hace más divertido, puesto que sabemos que el número a adivinar no puede estar en dos tarjetas consecutivas. Una vez que nos señalen que el número está en una tarjeta sabemos, gracias al teorema de Zeckendorf, que no estará en la siguiente. Esto nos permite escoger entre el auditorio a algunas personas con “derecho a no decir la verdad”, a las que podremos preguntar justo después de que algún sincero haya señalado una tarjeta en la que aparece el número. Esto dará la apariencia de que nos ponen el juego más difícil al no saber si toda la información es cierta o no.
He escrito esta entrada gracias a Antonio Aranda y Ramón Piedra.
El test de Turing o la inteligencia de las máquinas
Visto en la sección Diario Turing de eldiario.es
Alan Turing fue un visionario y siempre creyó en que las máquinas podrían evolucionar logrando una inteligencia artificial. Para exponer su tesis de las máquinas pensantes ideó el juego de imitación, lo que hoy conocemos como el test de Turing
“Si una máquina se comporta en todos los aspectos como inteligente, entonces debe ser inteligente”. Esta premisa, y casi convicción, llevó a Alan Turing a exponer en la prestigiosa revista filosófica Mind su pensamiento ante la comunidad científica británica. Su artículo, publicado en 1950 bajo el título “Computing machinery and intelligence”, ahondaba sobre la inteligencia artificial haciéndose una sencilla y trascendental pregunta: ¿pueden las máquinas pensar?
Turing proponía en ese artículo lo que hoy se conoce como el test de Turing, y que consistía en llevar a cabo el juego de imitación. Para dicho juego es necesario un juez, ubicado en una habitación aislada, y un individuo y una máquina en otra. Ambos responderán por chat a la preguntas que les realice el interrogador. La máquina ha de hacerse pasar por un ser humano; si el juez es incapaz de distinguir entre el individuo y el ordenador, se considera entonces que la máquina ha alcanzado un determinado nivel de madurez: es inteligente.
Para Turing, la inteligencia artificial existirá cuando no seamos capaces de distinguir entre un ser humano y un programa de una computadora en una conversación a ciegas.
Pero la década de los cincuenta estaba lejos de ser una época en la que las ideas visionarias de Turing tuvieran cabida fácilmente. Tuvo que enfrentar críticas y comentarios –a los que respondía en el citado artículo– del ámbito teológico (Dios no ha dotado a los animales ni a las máquinas de alma), pero también matemático. Los colegas matemáticos dudaban de que una máquina pudiera contestar a preguntas que escaparan del sí o del no y que pudieran emular el intelecto humano.
De ELIZA a CAPTCHA
Más de diez años después del polémico artículo, un profesor emérito de informática del MIT, Joseph Weizenbaum, diseñó uno de los primeros programas en procesar lenguaje natural. ELIZA, inspirado en los postulados de Alan Turing, funcionaba buscando palabras clave en las frases escritas por el usuario y respondiendo con una frase modelo registrada en su base de datos.
Resultó tan convincente que algunas personas que interactuaron con el programa, sin saberlo, llegaron a pensar que realmente hablaban con un humano. Aunque ELIZA tenía sus límites: cuando no entendía el enunciado, repetía las palabras en forma de frases y expresiones incoherentes. Aún quedaba mucho para lograr una máquina inteligente.
En 1990 se inició el concurso Premio Loebner entre programas de ordenador que intentan pasar el test de Turing. Un juez humano se enfrenta a dos pantallas de ordenador, una de ellas se encuentra bajo el control de un ordenador, y la otra, bajo el control de un humano. El juez plantea preguntas a las dos pantallas y recibe respuestas.
El premio, que se celebra de forma anual, está dotado con 100.000 dólares para el programa que pase el test. La primera y única vez que un juez confundió a una máquina con un humano fue en el año 2010, cuando el robot Suzette, de Bruce Wilcox, superó la prueba.
Actualmente, una de las aplicaciones de la prueba de Turing más extendida es el control de spam. Este correo basura es generalmente enviado por un ordenador, así que el test de Turing puede usarse para distinguir si el remitente es humano o una máquina. El CAPTCHA, Completely Automated Public Turing test to tell Computers and Humans Apart (prueba de Turing pública y automática para diferenciar máquinas y humanos), esa conocida sucesión de números y letras, su ‘juez’ es, paradójicamente, un ordenador.
Las predicciones de Turing sobre máquinas y el juego de imitación son todavía un desafío. El matemático pensaba que en unos 50 años las máquinas jugarían tan bien que un interrogador no podría realizar la adecuada identificación tras cinco minutos de preguntas. La inteligencia artificial sería algo común y corriente.
“Creo –decía Turing– que a finales de siglo la opinión educada general se habrá modificado de tal manera que se podrá hablar de máquinas que piensan sin esperar que lo contradigan”.
No hagas en Internet lo que no harías en persona
El experto en criptografía Luis Hernández Encinas interviene en Hablan los científicos
Inventar métodos más seguros para enviar información cifrada –es decir, oculta, salvo para su destinatario autorizado– es la principal tarea de Luis Hernández Encinas. Aunque su trabajo recuerde al de los espías de películas y novelas del género, las apariencias engañan. Este matemático dirige el departamento de Tratamiento de la Información y Criptografía del Instituto de Tecnologías Físicas y de la Información ‘Leonardo Torres Quevedo’ (CSIC). Explicar lo que allí hacen investigadores de diferentes campos no es tarea sencilla. “Es complicado bajar al nivel del ciudadano de a pie cuando habitualmente manejas fórmulas y algoritmos”, explica. Pero Hernández no se resigna. Hasta cuatro veces ha participado en la Semana de la Ciencia con talleres para enseñar herramientas criptográficas al alcance de cualquiera, cómo utilizar el DNI electrónico o el funcionamiento de la mítica máquina Enigma. “Tenemos que saber transmitir las maravillas de la ciencia. El problema es que no tenemos una infraestructura para ello”, señala. En esta entrevista Hernández habla sobre la necesidad de más divulgación científica y también sobre las actuales amenazas a la ciberseguridad, los escándalos por el espionaje de EEUU o las cautelas que deben tener los ciudadanos en Internet.
Eres experto en criptografía, concretamente en generación de números pseudoaleatorios, criptografía de clave pública, criptosistemas basados en curvas elípticas, firmas electrónicas… ¿Cómo se traduce esto al lenguaje cotidiano?
Me dedico a todo lo que tiene que ver con los procesos de cifrar información, es decir, ocultarla para que solo el destinatario autorizado a recibirla sea capaz de recuperarla. Por ejemplo, si queremos enviar un documento cuyo contenido debe ser confidencial, lo que hacemos es modificarlo con algoritmos matemáticos y con una clave. Después se lo enviamos al destinatario y este, conociendo la clave adecuada, accederá a la información del mensaje original. Pero siempre habrá que asumir que el envío no es seguro porque alguien a mitad del camino puede lograr acceder al documento modificado. Hay que conseguir que al menos no sea capaz de descifrarlo.
¿Para qué se utilizan estos procedimientos?
Son utilizados por todos aquellos ciudadanos que quieren que la información que envíen sea confidencial. También por el mundo empresarial -cuando se intercambia información sobre planes de negocio-, por bancos y en todo lo que son las relaciones con la Administración pública electrónica. Por ejemplo, para obtener tu padrón municipal tendrás que identificarte. Para ello tiene que haber un protocolo criptográfico que asergure que tú eres quien dices ser.
¿Qué conocimientos teóricos tenéis los investigadores que os dedicáis a la criptografía?
La criptografía cae dentro de varios campos: matemáticas, física, telecomunicaciones, informática… Todo lo que tiene que ver con las ciencias de la computación. Pero una parte muy importante, la relativa a los algoritmos, son matemáticas. Continuar leyendo “No hagas en Internet lo que no harías en persona”