Acabamos de subir, tanto a la plataforma de enseñanza virtual como a este blog, los apuntes del tema 2 y la correspondiente relación de problemas.
Estos apuntes son aún susceptibles de sufrir pequeñas mejoras que no modificarán su contenido.
Archivo de la categoría: Teoría
Primera sesión de recuperación para repetidores
La primera sesión de recuperación para repetidores será este viernes 30 de septiembre a las 15:30 en el aula 0.2.
Para participar será imprescindible haber trabajado la autoevaluación del tema 1 que se colgó la semana pasada en este blog.
NOTA: La participación en estas sesiones no forma parte de la evaluación y, por tanto, no implicará una calificación que pueda ser tenida en cuenta de cara a la tercera convocatoria.
Acciones de recuperación para repetidores
Pensando en aquellos estudiantes que no hayan superado la asignatura el pasado curso vamos a impartir cuatro sesiones, una por cada tema, fuera del horario de clases. Esta acción está dirigida principalmente a aquellos que se estén planteando presentarse a la “convocatoria de diciembre” (que de hecho será el 16 de noviembre), aunque está abierta a todo el alumnado.
Las fechas previstas para estas sesiones son el 30 de septiembre (tema 1), 14 de octubre (tema 2), 28 de octubre (tema 3) y 11 de noviembre (tema 4). Será en horario de tarde (a primera hora), aunque la hora exacta y el lugar de cada sesión se comunicarán más adelante por este medio.
Para hacer más provechosas estas sesiones, antes de cada una se propondrán pruebas de autoevaluación, consistentes en problemas y cuestiones teóricas, que habrán de hacerse individualmente con anterioridad a cada sesión.
Para participar en este programa cada alumno deberá inscribirse enviando un correo electrónico al profesor de su grupo antes del lunes 26.
NOTA: La participación en estas sesiones no forma parte de la evaluación y, por tanto, no implicará una calificación que pueda ser tenida en cuenta de cara a la tercera convocatoria.
Relación de problemas del tema 1
Acaba de subirse a este blog la relación de problemas del tema 1.
También se ha sustituido el fichero con los apuntes del tema 1 por otro con pequeñas correcciones.
Bienvenidos al curso 2016-17
Bienvenidos los nuevos estudiantes a este blog de la asignatura Álgebra Básica. Aquí iremos enlazando todo el contenido que se pondrá a vuestra disposición. También publicaremos anuncios, noticias relevantes y alguna que otra cosa.
Para comenzar, en la página Material de la asignatura. Curso 16-17 hemos enlazado: el extracto del proyecto docente que se está repartiendo en clase el primer día; unas notas Preliminares con algunos conceptos que es bueno conocer porque pueden ser útiles para el desarrollo de la asignatura, pero que no explicaremos en clase, y las notas de teoría del primer tema de Conjuntos.
Las notas del primer tema están aún siendo revisadas y pueden sufrir pequeñas modificaciones.
Material del tema 4
Apuntes del tema 3
Acabamos de subir a este blog las notas de teoría del tema 3 y la presentación.
Corrección en los apuntes del tema 2
Se han corregido los apuntes del tema 2. Concretamente se ha eliminado el siguiente ejercicio que se había propuesto con cierta ligereza:
Este resultado se puede extender a grupos finitos en general. Si \((G,\star )\) es un grupo finito que tiene algún elemento de orden impar, entonces tiene tantos elementos de orden par como impar.
Lo que propone el ejercicio es falso. Invitamos al lector a buscar un ejemplo de grupo que tenga todos sus elementos de orden impar.
El ejercicio eliminado estaba en la página 67 de los apuntes y aparecía etiquetado como “Ejercicio 2.4.6”.
Lo que sí es cierto, tras demostrar el Teorema de Cayley, es que en cada grupo finito, al ser isomorfo a un subgrupo de \(S_n\), debe existir una clasificación análoga a la del signo en las permutaciones. Pero esta clasificación no es la paridad del orden de los elementos.
Material del tema 2
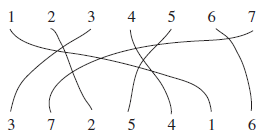Se acaba de subir a este blog (y a la plataforma de enseñanza virtual) la presentación que uso en mis clases para la explicación del tema 2. Está en la página MATERIAL DE LA ASIGNATURA CURSO 15/16.
Además se han modificado las notas de teoría del tema 2. Concretamente se han corregido las permutaciones que intervienen en la explicación del juego inicial (página 58 y siguientes), que estaban mal, y la del ejemplo 2.3.15. Además se ha añadido una observación tras la fórmula de Cauchy en la página 63, la nota 2.3.19.
Apuntes de teoría de grupos
Acabo de subir a la red las notas de teoría correspondientes al Tema 2: Introducción a la teoría de grupos.