Hay que reconocer que se nos ha ido un poco la mano con la autoevaluación del tema 2. Hay algún ejercicio difícil y, sobre todo, es demasiado larga. Acabamos de subir a Material de la Asignatura la solución, para que se pueda contrastar qué se ha hecho bien y cómo se hace aquello que no se ha sabido hacer.

Se ha añadido en la página Material de la asignatura un enlace a una autoevaluación del tema 2. Mañana pondremos la solución.

En la serie Futurama, el episodio 10 de la sexta temporada, El prisionero de Benda, es un poco especial. Tan especial, que merece la pena que hablemos de él en Álgebra Básica. Al fin y al cabo, no en muchas series aparecen teoremas originales, correctamente enunciados, y correctamente demostrados.

En este capítulo ocurren muchas cosas, pero el argumento esencial es que el Profesor Farnsworth y Amy construyen una máquina que les permite intercambiar sus mentes. Así, cada uno puede hacer cosas que no podría en su cuerpo original. (No haré más spoilers que éste.)

Por desgracia, la máquina no funciona dos veces sobre los mismos cuerpos. En términos de permutaciones (este sigue siendo el blog de Álgebra Básica, después de todo), si representamos el intercambio del profesor y Amy como una trasposición, tenemos que una vez que se usa la trasposición \((pa)\), ya no se puede volver a usar.

Naturalmente, como Futurama es Futurama, la cosa se desmadra bastante, y tras una muy complicada serie de acontecimientos, hay que deshacer cambios entre Amy, el Profesor Farnsworth, el Emperador Nikolai, Bender, el robot cubo de limpieza, Leela, Fry, Zoidberg, Hermes y Scrufy. ¿Cómo resolverlo?

En palabras del Profesor Farnsworth (hablando desde el cuerpo de Bender),

I’m afraid we need to use… math!
Profesor Farnsworth

El autor de este capítulo resulta ser Ken Keeler, casualmente un matemático doctorado por la Universidad de Harvard. Para reolver el capítulo, Keeler demostró el siguiente Teorema:

En el capítulo, \(x\) e \(y\) son dos personajes nuevos, dos globertrotters que demuestran el teorema y consiguen devolver cada mente a su cuerpo (o al revés, ya no me queda claro).

El teorema, y su demostración correcta y completa, aparece en una imagen del episodio: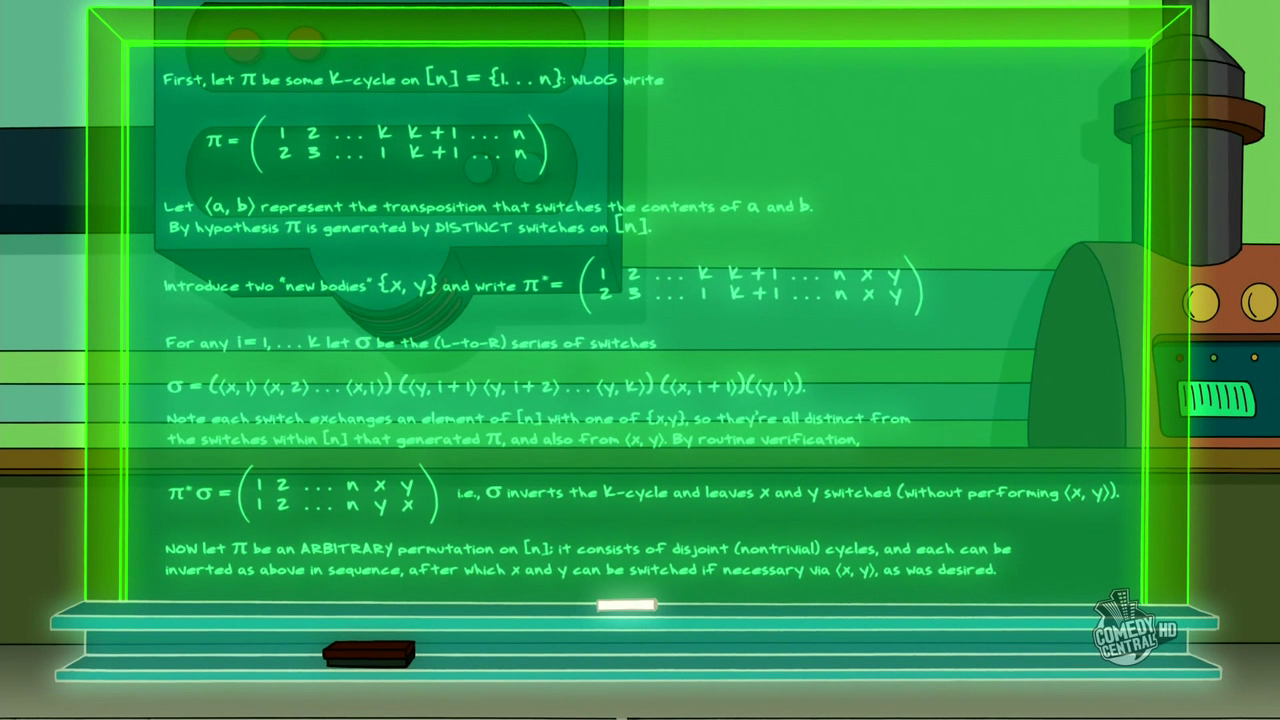

Se puede seguir fácilmente la demostración escrita en la imagen, así que no haré más que un par de comentarios.

1. En primer lugar, como toda permutación se descompone en producto de ciclos disjuntos, basta demostrar el Teorema para un ciclo \(\pi\), que se puede escribir, sin pérdida de generalidad como
   $$
   \pi =\begin{pmatrix}
   1 & 2 & \dots &k &k+1 &\dots& n \\
   2 & 3 & \dots & 1 & k+1 &\dots &n
   \end{pmatrix}.
   $$
2. En la demostración, por comodidad se escribe el producto de permutaciones de izquierda a derecha, mientras que nosotros, en clase, usamos el producto de derecha a izquierda.

Me había planteado poner este teorema como ejercicio del primer parcial, pero en fin, me han convencido para que no lo haga, al menos este año.

¿Conocéis otros ejemplo de un teorema correctamente demostrado en una serie o película? No vale si están sólo enunciados…

Aquí tenéis un vídeo (en inglés) que comenta con bastante más detalle el capítulo y el enunciado del Teorema, aunque no cubre la demostración.

Hace unos días, comenté en clase de pasada que existe un teorema de clasificación de grupos finitos, y dije (de cabeza) que el teorema tiene aproximadamente 15.000 páginas. No era un error, pero quizá sea interesante dar algunos detalles adicionales.

Subgrupos normales… y de los otros.

En primer lugar, hace falta definir lo que es un subgrupo normal. Dado un grupo \((G,\star)\), se dice que \(H\subset G\) es un subgrupo si para todo elemento \(g\in G\) se verifica que \(g\star H=H\star g\). Obviamente, si el grupo \(G\) es conmutativo, todos sus subgrupos son normales. Pero eso no es necesariamente cierto si \(G\) no es conmutativo.

Ejercicio: Demuestre que \(H=\{(),(12)\}\) es un subgrupo NO normal de \(S_3\). Demuestre que el grupo alternado \(A_3\) sí es un subgrupo normal de \(S_3\).

[Indicaciones: para la primera parte, calcule \((123)H\neq H(123)\). Para la segunda, observe que \(\sigma A_3\) sólo puede ser, bien\(A_3\), bien el conjunto de todas las permutaciones impares.]

Subgrupos simples… y de los otros.

Un grupo se llama simple si no tiene subgrupos normales. Si un grupo no es simple, se puede “romper” en dos grupos más pequeños; un subgrupo normal y el grupo cociente. A su vez, cada uno de estos grupos se pueden “romper” en grupos más pequeños y así sucesivamente. Si \(G\) es un grupo finito, es claro que en algún momento llegaremos a expresar \(G\) en función de grupos simples. El resultado preciso es más complicado de enunciar, se llama Teorema de Jordan-Hölder.

El resumen de todo esto es que para clasificar los grupos finitos, basta clasificar los grupos finitos simples. Para saber más, puede empezar por la wikipedia, o por un artículo de Richard Elwes sobre el tema.

El mega-Teorema.

Pues bien, existe un Teorema de Clasificación de grupos simples finitos, distribuido a lo largo de 15.000 páginas, que dice, esencialmente, que un grupo finito simple es isomorfo a uno de los siguientes tipos¹:

1. Grupos cíclicos de orden primo.
2. Grupos alternados \(A_n\), con \(n\geq 5\).
3. Grupos (de tipo Lie) de Chevalley
4. Otros grupos (de tipo Lie): grupos de Chevalley torcidos (twisted) o grupo de Tits.
5. Grupos esporádicos. Aquí aparecen 26 grupos “inclasificables”. Entre éstos, encontramos nombres tan curiosos como baby monster, monster, los grupos parias, etc.

El grupo monster se llama así no por la bebida energética, sino porque es el grupo simple finito más grande. Además, contiene 20 de los 26 grupos esporádicos como subcocientes. Los seis que no están contenidos son los “parias”. El grupo monster es finito, pero poco: tiene orden

\(808017424794512875886459904961710757005754368000000000.\)

¡Sí que da miedo el monster!