En la serie Futurama, el episodio 10 de la sexta temporada, El prisionero de Benda, es un poco especial. Tan especial, que merece la pena que hablemos de él en Álgebra Básica. Al fin y al cabo, no en muchas series aparecen teoremas originales, correctamente enunciados, y correctamente demostrados.
En este capítulo ocurren muchas cosas, pero el argumento esencial es que el Profesor Farnsworth y Amy construyen una máquina que les permite intercambiar sus mentes. Así, cada uno puede hacer cosas que no podría en su cuerpo original. (No haré más spoilers que éste.)
Por desgracia, la máquina no funciona dos veces sobre los mismos cuerpos. En términos de permutaciones (este sigue siendo el blog de Álgebra Básica, después de todo), si representamos el intercambio del profesor y Amy como una trasposición, tenemos que una vez que se usa la trasposición \((pa)\), ya no se puede volver a usar.
Naturalmente, como Futurama es Futurama, la cosa se desmadra bastante, y tras una muy complicada serie de acontecimientos, hay que deshacer cambios entre Amy, el Profesor Farnsworth, el Emperador Nikolai, Bender, el robot cubo de limpieza, Leela, Fry, Zoidberg, Hermes y Scrufy. ¿Cómo resolverlo?
En palabras del Profesor Farnsworth (hablando desde el cuerpo de Bender),
I’m afraid we need to use… math!
Profesor Farnsworth
El autor de este capítulo resulta ser Ken Keeler, casualmente un matemático doctorado por la Universidad de Harvard. Para reolver el capítulo, Keeler demostró el siguiente Teorema:
Teorema (Teorema de Futurama, K. Keeler)
Sea \(A\) un conjunto finito y sean \(x\) e \(y\) dos elementos que no pertenecen a \(A\). Toda permutación de \(A\) se puede reducir a la identidad mediante una sucesión de trasposiciones de \(A\cup \{x,y\}\) cada una de las cuales contiene a \(x\) o a \(y\).
En el capítulo, \(x\) e \(y\) son dos personajes nuevos, dos globertrotters que demuestran el teorema y consiguen devolver cada mente a su cuerpo (o al revés, ya no me queda claro).
El teorema, y su demostración correcta y completa, aparece en una imagen del episodio: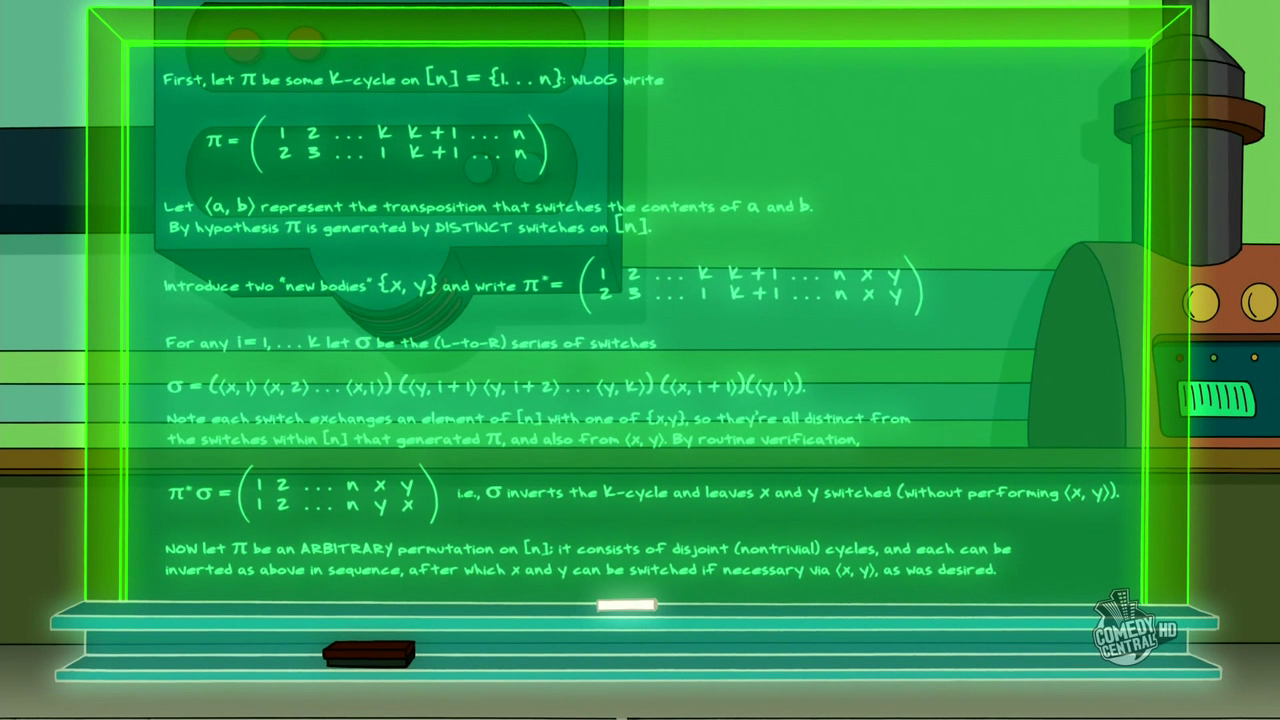
Se puede seguir fácilmente la demostración escrita en la imagen, así que no haré más que un par de comentarios.
- En primer lugar, como toda permutación se descompone en producto de ciclos disjuntos, basta demostrar el Teorema para un ciclo \(\pi\), que se puede escribir, sin pérdida de generalidad como
$$
\pi =\begin{pmatrix}
1 & 2 & \dots &k &k+1 &\dots& n \\
2 & 3 & \dots & 1 & k+1 &\dots &n
\end{pmatrix}.
$$ - En la demostración, por comodidad se escribe el producto de permutaciones de izquierda a derecha, mientras que nosotros, en clase, usamos el producto de derecha a izquierda.
Me había planteado poner este teorema como ejercicio del primer parcial, pero en fin, me han convencido para que no lo haga, al menos este año.
¿Conocéis otros ejemplo de un teorema correctamente demostrado en una serie o película? No vale si están sólo enunciados…
Aquí tenéis un vídeo (en inglés) que comenta con bastante más detalle el capítulo y el enunciado del Teorema, aunque no cubre la demostración.
