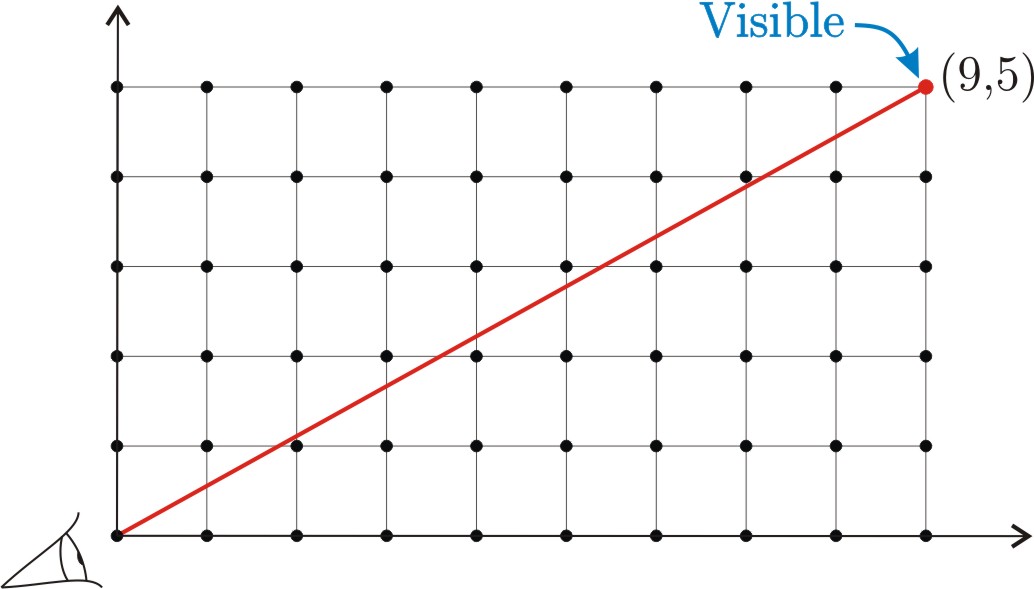
Hay una forma muy visual de demostrar propiedades de los números primos. Consideremos los puntos del plano con coordenadas enteras positivas. Diremos que uno de esos puntos \((m,n)\) es visible desde el origen de coordenadas si no hay ningún otro punto con coordenadas enteras en el segmento que une \((0,0)\) y \((m,n)\). Es decir, si nos ponemos en \((0,0)\), no hay nigún otro punto que nos tape la vista de \((m,n)\).
(Para los listos: un punto es visible si y sólo si sus coordenadas son coprimas.)
Si un número primo es aquel entero \(p>1\) cuyos únicos divisores positivos son 1 y \(p\), veamos cómo podemos demostrar, usando los puntos visibles, la siguiente propiedad fundamental de los números primos:
Lema de Euclides: Si un primo \(p\) divide a un producto \(ab\), o bien \(p\) divide a \(a\), o bien \(p\) divide a \(b\).
Este resultado suele demostrarse usando la identidad de Bezout, que a su vez se suele deducir del algoritmo de Euclides. Pero nosotros lo demostraremos de forma más visual, a ver si esto ayuda a que los incrédulos queden convencidos…
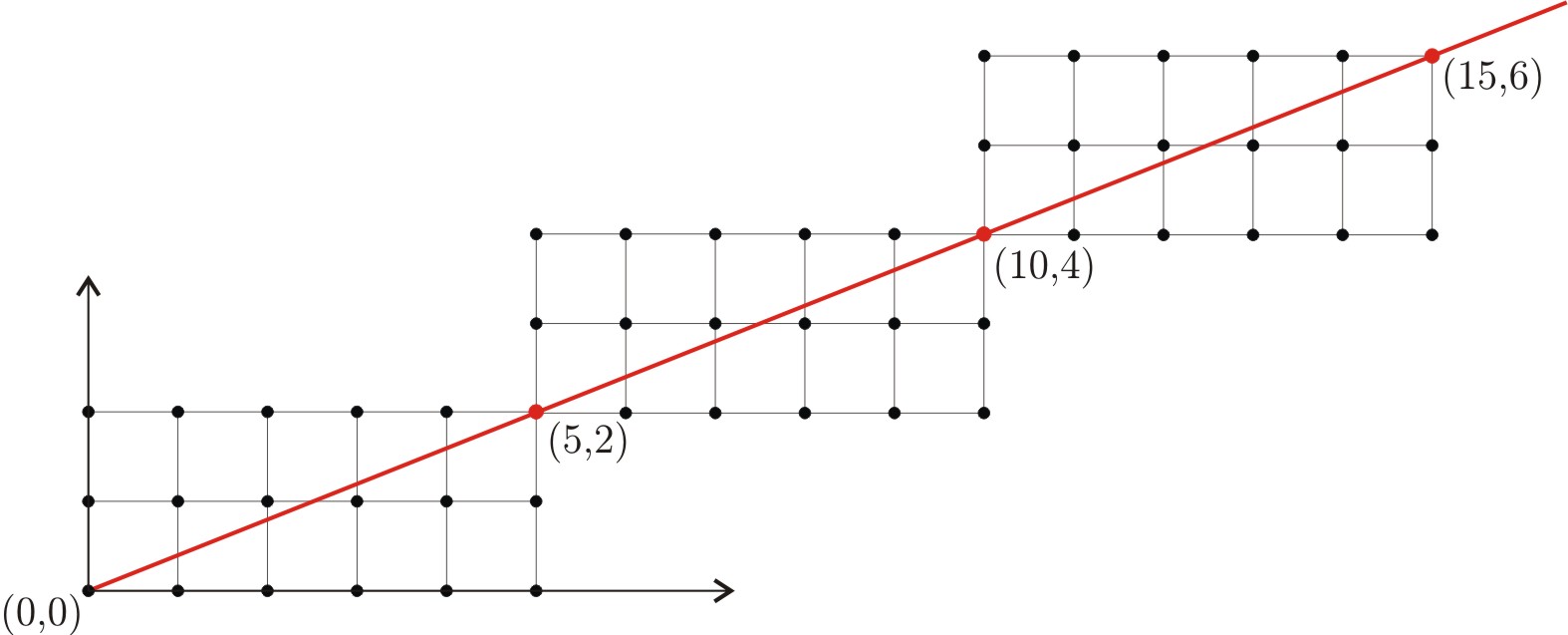
En primer lugar, observemos que si trazamos una semirrecta desde \((0,0)\) en el primer cuadrante, y encuentra un punto visible con coordenadas enteras \((m,n)\), entonces los puntos con coordenadas enteras de esa semirrecta son precisamente los de la forma \((qm,qn)\) para todo número natural \(q\), ya que el dibujo que hizo la semirrecta hasta llegar a \((m,n)\) se repite indefinidamente.
Observemos el punto \((a,p)\). Quizás no sea visible. En este caso el segmento que va de \((0,0)\) a \((a,p)\) tendría un punto visible \((m,n)\) con \(n<p\), por lo que \((a,p)=(qm,qn)\) para algún \(q\). Como \(n\) divide a \(p\), que es primo, y es menor que él, debe ser \(n=1\). Luego \(p=q\) y por tanto \(a=pm\). Es decir, en este primer caso \(p\) divide a \(a\).
Queda el otro caso: que el punto \((a,p)\) sea visible. En este caso, los puntos con coordenadas enteras de la semirrecta que sale de \((0,0)\) y pasa por \((a,p)\) son los de la forma \((qa,qp)\) para todo número natural \(q\). Ahora simplemente tenemos que observar que el punto \((\frac{ab}{p},b)\) tiene coordenadas enteras (porque \(p\) divide a \(ab\)), y pertenece a la semirecta (porque es proporcional a \((a,p)\)). Por tanto, si miramos la segunda coordenada tenemos \(b =qp\), es decir \(p\) divide a \(b\).
QED



 En un pueblo con \(12 k\) habitantes, cada uno conoce a \(3k+6\) convecinos y el conocimiento es mutuo. Existe un entero positivo \(n\) tal que, para cada pareja de habitantes, el número de personas que conocen a ambos es \(n\). ¿Cuántos habitantes hay en el pueblo?
En un pueblo con \(12 k\) habitantes, cada uno conoce a \(3k+6\) convecinos y el conocimiento es mutuo. Existe un entero positivo \(n\) tal que, para cada pareja de habitantes, el número de personas que conocen a ambos es \(n\). ¿Cuántos habitantes hay en el pueblo?