Curiosidades – Página 6 – Blog del Departamento de Álgebra

El teorema de Zeckendorf o “Magia y Fibonacci”

De lo que hablamos hoy aquí ya se habló en Divulgamat y ZTFNews.org,
y también en Gaussianos.

Edouard Zeckendorf fue un médico, oficial del ejercito y matemático belga que, en 1972, publicó el siguiente teorema:

Todo número entero positivo puede representarse de forma única como suma de números de Fibonacci (esto es, elementos de la sucesión de Fibonacci) distintos, de tal forma que dicha representación no contiene dos números de Fibonacci consecutivos.

Esta representación se denomina representación de Zeckendorf del número entero positivo en cuestión.

La demostración de la existencia se realiza por inducción. Dicho muy esquemáticamente, se supone el resultado cierto para cualquier entero positivo menor que uno dado $N$, se escoge el mayor número de Fibonacci $F_j$ menor o igual que $N$ y se aplica la inducción al número $N-F_j$.

Así, para obtener la representación de Zeckendorf de $1954$, escogemos el mayor número de la sucesión que sea menor o igual que $1954$, ya saben, $1597$. La diferencia es $1954-1597=357$. Ahora el número de Fibonacci más cercano a $357$ es $233$. Restando $357-233=124$. Escogemos $89$ como el siguiente número de Fibonacci en la representación de Zeckendorf, $124-89=35$. Como $34$ está en la sucesión de Fibonacci, la representación es:

$1954=1597+233+89+34+1$.

(Por supuesto, para la representación de Zeckendorf no contamos el $atex 0$ y sólo tomamos uno de los dos términos iguales a $1$)

La unicidad se basa en el siguiente lema:

La suma de cualquier conjunto no vacío de números de Fibonacci, no consecutivos, cuyo mayor elemento sea $F_j$, es estrictamente menor que el siguiente término $F_{j+1}$.

Una aplicación curiosa de esta representación es el paso de millas a kilómetros y viceversa. Dado que la razón aúrea es

$\displaystyle\varphi\approx 1’6181033\ldots =\lim_{n\to\infty}\frac{F_n}{F_{n+1}}$,

muy parecida a la razón entre millas y kilómetros: $1’6093$, para pasar (aproximadamente) $N$ millas a kilómetros se puede sustituir cada término en la representación de Zckendorf de $N$ por su siguiente en la sucesión de Fibonacci. Es decir

$1954=1597+233+89+34+1$ millas

son aproximadamente

$3162=2584+377+144+55+2$ kilómetros.

Otra aplicación del teorema es el siguiente juego, que consiste en adivinar cualquier número que el auditorio haya pensado entre $1$ y $100$. Para ello, una vez que se han puesto de acuerdo, a tus espaldas, en escoger un número, tú les vas presentando una por una estas 10 tarjetas con números “aleatorios”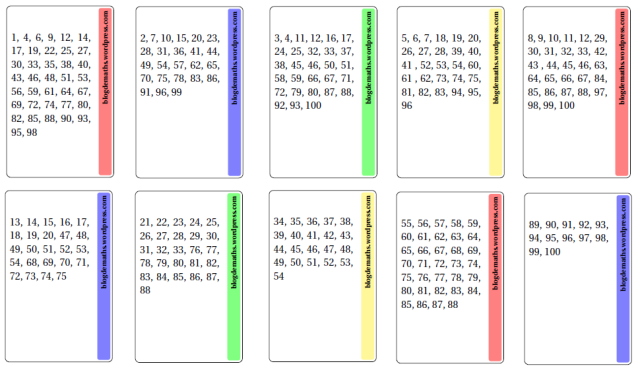y ellos tienen que decir si su número se encuentra en ellas o no. Astútamente estas tarjetas las hemos fabricado de tal forma que comienzan por un número de Fibonacci, que está seguido por todos aquellos, mayores que él, que lo contienen en su representación de Zeckendorf.

Por ejemplo, si el número que han pensado es $32$ escogerán las siguientes tarjetas y nosotros sólo tendremos que sumar los primeros números de cada tarjeta, 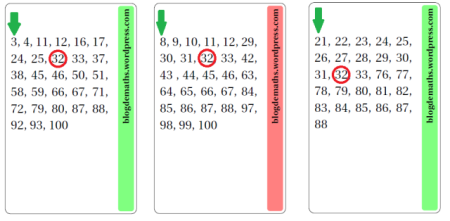pues la representación de Zeckendorf de $32$ es $32=21+8+3$.

El juego admite una variante que lo hace más divertido, puesto que sabemos que el número a adivinar no puede estar en dos tarjetas consecutivas. Una vez que nos señalen que el número está en una tarjeta sabemos, gracias al teorema de Zeckendorf, que no estará en la siguiente. Esto nos permite escoger entre el auditorio a algunas personas con “derecho a no decir la verdad”, a las que podremos preguntar justo después de que algún sincero haya señalado una tarjeta en la que aparece el número. Esto dará la apariencia de que nos ponen el juego más difícil al no saber si toda la información es cierta o no.

He escrito esta entrada gracias a Antonio Aranda y Ramón Piedra.

Poliedros de Goldberg ¿una nueva clase de sólidos?

Recientemente los investigadores Stan Schein y James Maurice Gayed, de la Universidad de California Los Ángeles, parecen haber descubierto la existencia de un nuevo tipo de sólido geométrico. Schein y Gayed se han inspirado en el trabajo de Michael Goldberg, quien describió en 1937 un conjunto de cuerpos geométricos que se conocieron como poliedros de Goldberg, pese a que en realidad no eran poliedros ya que no tenían su caras planas (tenían ángulos internos). Los investigadores Schein y Gayed afirman haber encontrado una forma de conseguir que estos ángulos internos sean cero, lo cual implica que las caras son planas y se trata de verdaderos poliedros (aunque en el proceso las caras hexagonales dejan de ser regulares). Schein encontró estas formas estudiando una proteína llamada Clatrina, esta vez con caras planas. En honor al trabajo de Goldberg, han decidido llamar a estos nuevos sólidos, “poliedros de Goldberg”.

Este nuevo tipo de poliedros podría tener diversas aplicaciones, desde mejorar la aerodinámica de una pelota de golf hasta el desarrollo de nuevos fármacos —algunos virus, como el de la gripe, tienen una forma similar al poliedro de Goldberg.

Pueden encontrar en ScienceNews más información.

S. Schein and J.M. Gayed. Fourth class of convex equilateral
polyhedron with polyhedral symmetry related to fullerenes and
viruses. Proceedings of the National Academy of Sciences. Published
online February 10, 2014. doi: 10.1073/pnas.1310939111.

Las matemáticas revelan cómo conseguir que internet sea más resistente a los terremotos

Visto en MIT Technology Review

Las redes descentralizadas son, por naturaleza, resistentes a determinados tipos de ataques. Ahora un matemático afirma que la geometría avanzada nos demuestra cómo hacer que sean aún más resistentes

Uno de los mitos comúnmente aceptados sobre internet es que se diseñó durante la Guerra Fría para sobrevivir a un ataque nuclear. Los historiadores de internet se apresuran a señalar que éste no era uno de los objetivos a la hora de diseñar la primera red, aunque la naturaleza descentralizada del sistema hace que sea mucho más robusto que cualquier clase de red centralizada.

A pesar de todo, internet sigue siendo vulnerable. Sirvan como ejemplo el terremoto de magnitud 9 en la escala de Richter y el tsunami resultante que golpearon Japón el 11 de marzo de 2011, produciendo graves daños en la infraestructura de telecomunicaciones japonesa.

La empresa de telecomunicaciones japonesa NTT afirma que perdió 18 puntos de intercambio y 65.000 postes de teléfono en el desastre, que además dañó 1,5 millones de circuitos de línea fija y 6.300 kilómetros de cables.

Así pues, surge una pregunta interesante: ¿se podría reforzar el planteamiento espacial de internet contra este tipo de daños?

Hay una posible respuesta en el trabajo del investigador Hiroshi Sato en los Laboratorios de Tecnología de Red de NTT en Tokio (Japón). Saito ha calculado la probabilidad de que una red quede dañada en un desastre dependiendo de su geometría espacial. Es decir, ha averiguado cómo determina la forma de una red sus probabilidades de acabar mal.

Saito comienza imaginando una red que contiene un área finita en la que sucede un desastre como un terremoto, por ejemplo. Los nodos en este área tienen una probabilidad determinada de fallar. La pregunta es cuál es la mejor forma de organizar los nodos para minimizar la probabilidad de que crucen un área catastrófica si ésta sucede.

La salsa matemática secreta usada por Saito para probar sus resultados es una disciplina que se conoce como geometría integral. La usa para demostrar hábilmente una serie de reglas de buen cubero que los científicos de red pueden aprovechar fácilmente. “Este método teórico revela explícitamente reglas de diseño de redes físicas resistentes a los terremotos”, afirma.

Por ejemplo, una ruta que pase por varios nodos, tiene inevitablemente forma de zigzag. Una regla es que los zigzags más cortos reducen la probabilidad de que una red intersecte una zona catastrófica. Otra es que si la red forma un anillo las rutas adicionales dentro del anillo no reducen la probabilidad de que todas las rutas entre un par de nodos intersecten la zona de desastre.

A continuación prueba estas ideas usando los datos de intensidad de varios terremotos reales en Japón, todos ellos con una magnitud superior a 5 (en la escala japonesa sobre 7). Entre ellos el terremoto de 1995 de Kobe, que fue el segundo más destructivo de la historia de Japón.

(Pero no incluye los datos relativos al terremoto de 2011 puesto que ocurrió bajo el mar y la zona catastrófica no se puede contener completamente dentro de la red de telecomunicaciones. Este terremoto viola uno de los supuestos matemáticos básicos de sus pruebas).

Después superpuso varias redes sobre los datos relativos al terremoto y probó a ver qué tal les iría en cada caso. Los resultados demostraban que sus “reglas generales” teóricas deberían funcionar igual de bien en el mundo real que en la teoría. “Los resultados del análisis se validan con los datos empíricos de los terremotos”, afirma.

Es una forma completamente nueva de pensar en la fiabilidad de las redes. En la actualidad los ingenieros diseñan las redes para que en primer lugar queden protegidas del daño y en segundo lugar que sean relativamente fáciles de restaurar en el caso de que haya daños.

Pero el enfoque de Saito es más ambicioso. “El método de diseño propuesto es el primer paso en la gestión de desastres y su objetivo es evitar los desastres”, explica. En otras palabras, mejor evitar el desastre si puede ser.

Resulta interesante. Históricamente los terremotos han azuzado la innovación en las redes de telecomunicaciones. Por ejemplo, Japón aumentó de forma drástica la cantidad de enlaces de microondas en su red después de un gran terremoto en 1968 y empezó a usar estaciones móviles para comunicarse con los satélites de telecomunicaciones después de otro en 1993. ¿Podría generalizarse también el uso de las ideas de Saito?

Ref: arxiv.org/abs/1402.6835 : El Diseño Espacial de Redes Físicas 
Resistentes a los Terremotos

La belleza de las Matemáticas (2)

Motivados por esta cita de Bertrand Russell, un equipo científico ha realizado un estudio, publicado en Frontiers in Human Neuroscience, en el que utilizaron imágenes de resonancia magnética funcional (fMRI) para visualizar la actividad cerebral de 15 matemáticos cuando observaban fórmulas matemáticas que habían calificado como hermosas, neutrales o feas.

Los resultados mostraron que la experiencia de la belleza matemática se correlaciona con la misma parte del cerebro, la corteza orbitofrontal medial, con la cual se vincula la percepción de belleza derivada del arte o de la música.

Como anécdota añadimos que la fórmula encontrada más bella por la mayoría de los matemáticos estudiados fue la identidad de Euler:

$1+e^{i\pi}=0,$

mientras que la que encontraron más fea fue la fórmula de Ramanujan que expresa el inverso de $\pi$ como una serie:

$\displaystyle\frac{1}{\pi}=\frac{2\sqrt{2}}{9801}\sum_{k=0}^{\infty}\frac{(4k)!(1103+26390k)}{(k!)^4296^{4k}} .$

Zeki S, Romaya JP, Benincasa DMT and Atiyah MF (2014) The experience
of mathematical beauty and its neural correlates.
Front. Hum. Neurosci. 8:68. doi: 10.3389/fnhum.2014.00068

¿Es cierto que 1+2+3+4+…=-1/12?

En los últimos días ha circulado bastante por las redes un vídeo del canal de Youtube Numberphile en el que el físico Tony Padilla da una “demostración” de que la suma de la serie $1+2+3+4+5+\ldots$ es igual a $-1/12$. Si no lo habéis visto aún, aquí lo tenéis:

En el vídeo, Padilla parte de la serie $1-1+1-1+\ldots$, que es sumable en cierto sentido y tiene como suma $1/2$ y, después de realizar algunas manipulaciones simples (sumas y restas, básicamente), llega al resultado anterior.

Pero ¿por qué quedarnos ahí? Vamos a seguir manipulando la suma de la misma forma que en el vídeo, a ver qué nuevas sorpresas obtenemos. Escribamos dos copias de la serie, la segunda de ellas desplazada un lugar:

$1+2+3+4+5+\ldots=-1/12$

$1+2+3+4+\ldots=-1/12$

Restando término a término, obtenemos $1+1+1+1+\ldots=0$. Un poco extraño, sí, pero después de saber que $1+2+3+4+5+\ldots=-1/12$, ya estamos curados de espanto. Repitamos ahora el proceso con esta nueva serie:

$1+1+1+1+1+\ldots=0$

$1+1+1+1+\ldots=0$

Ahora sí que la hemos liado: volviendo a restar, obtenemos que $1+0+0+0+\ldots = 0$, es decir $1=0$. Con lo cual, multiplicando por cualquier número $x$, obtenemos que $x=0$. Es decir: los números no existen, son todos el mismo. Nos acabamos de cargar todo el edificio de las matemáticas con un par de restas.

Moraleja: no todo lo que parece matemáticas es matemáticas. Al intentar demostrar algo, tenemos que ser extremadamente rigurosos y no dejarnos llevar por la intuición.

Pero entonces, ¿es cierta la fórmula o no? Pues, como pasa siempre en matemáticas, la pregunta no tiene sentido hasta que no definamos con precisión qué significa todo lo que aparezca en ella. En este caso, la respuesta depende de cómo se defina la suma $1+2+3+4+5+\ldots$. Con la definición habitual de convergencia de series en el marco del Análisis Matemático, el resultado es obviamente falso, puesto que la serie es divergente. Sin embargo, existen muchas deficiones alternativas de suma de una serie y algunas de ellas (como la sumación de Ramanujan) dan el valor $-1/12$ en este caso. La igualdad no tiene sentido si no especificamos qué método de sumación estamos usando. Decir que $1+2+3+4+5+\ldots$ es igual a $-1/12$ así, a secas, es incorrecto (por mucho que encaje en algunas fórmulas de la Física). Y lo que, desde luego, es incorrecto en cualquier caso es la “demostración” del vídeo.

Para leer más sobre el tema, recomiendo los excelentes posts del maestro Terence Tao en Google+ y en su blog.