Categoría: Retos

¡Tenemos ganador! Alberto Castaño, famoso divulgador con múltiples apariciones en los medios, después de estrujarse los sesos una sobremesa completa, y con la colaboración inestimable de Marta Aguilera, ha dado con una solución al problema. Un poquillo enrevesada, eso sí, pero correcta. La solución ganadora puede encontrarse en este fichero PDF. Pero si siguen leyendo, encontrarán una respuesta más sencilla, al más puro estilo de Warren Sánchez.

Recordemos el enunciado:

En un pueblo con \(12 k\) habitantes, cada uno conoce a \(3k+6\) convecinos y el conocimiento es mutuo. Existe un entero positivo \(n\) tal que, para cada pareja de habitantes, el número de personas que conocen a ambos es \(n\). ¿Cuántos habitantes hay en el pueblo?

Para resolver el problema, vamos a contar los habitantes del pueblo de dos maneras diferentes.

Por un lado, sabemos que hay \(12k\) vecinos. Por otro, habrá \({12k \choose 2} = 6k(12k-1)\) parejas, y cada una de ellas es conocida por \(n\) personas. Si contamos estas \(n\) personas \(6k(12k-1)\) veces, habremos contado a todo el pueblo, pero cada persona habrá sido contada varias veces. En concreto, cada vecino conoce a \({3k+6 \choose 2} = \frac{1}{2}(3k+6)(3k+5)\) parejas, luego habrá sido contado \(\frac{1}{2}(3k+6)(3k+5)\) veces.

Por tanto, el número de personas del pueblo es

\(\displaystyle\frac{6k(12k-1)n}{\frac{1}{2}(3k+6)(3k+5)} = \frac{12k(12k-1)n}{(3k+6)(3k+5)}\)

Como este número es igual a \(12 k\), obtenemos finalmente \((12k-1)n = (3k+6)(3k+5)\).

Ahora sólo queda saber qué números enteros pueden cumplir esta ecuación. Observemos que todo divisor común de \(12k-1\) y \(3k+6\), será también divisor de \(4(3k+6)-(12k-1)\), es decir, será divisor de 25. Igualmente, todo divisor común de \(12k-1\) y \(3k+5\) será también divisor de \(4(3k+5)-(12k-1)\), es decir, será divisor de 21. Por tanto, \(12k-1\) es obligatoriamente un divisor de \(25\times 21 = 525\).

Como el único divisor de 525 que se puede escribir de la forma \(12k-1\) es 35, debemos tener \(12k-1=35\), y por tanto el número de habitantes del pueblo es \(12k =36\). ¡Una aldeíta, vamos!

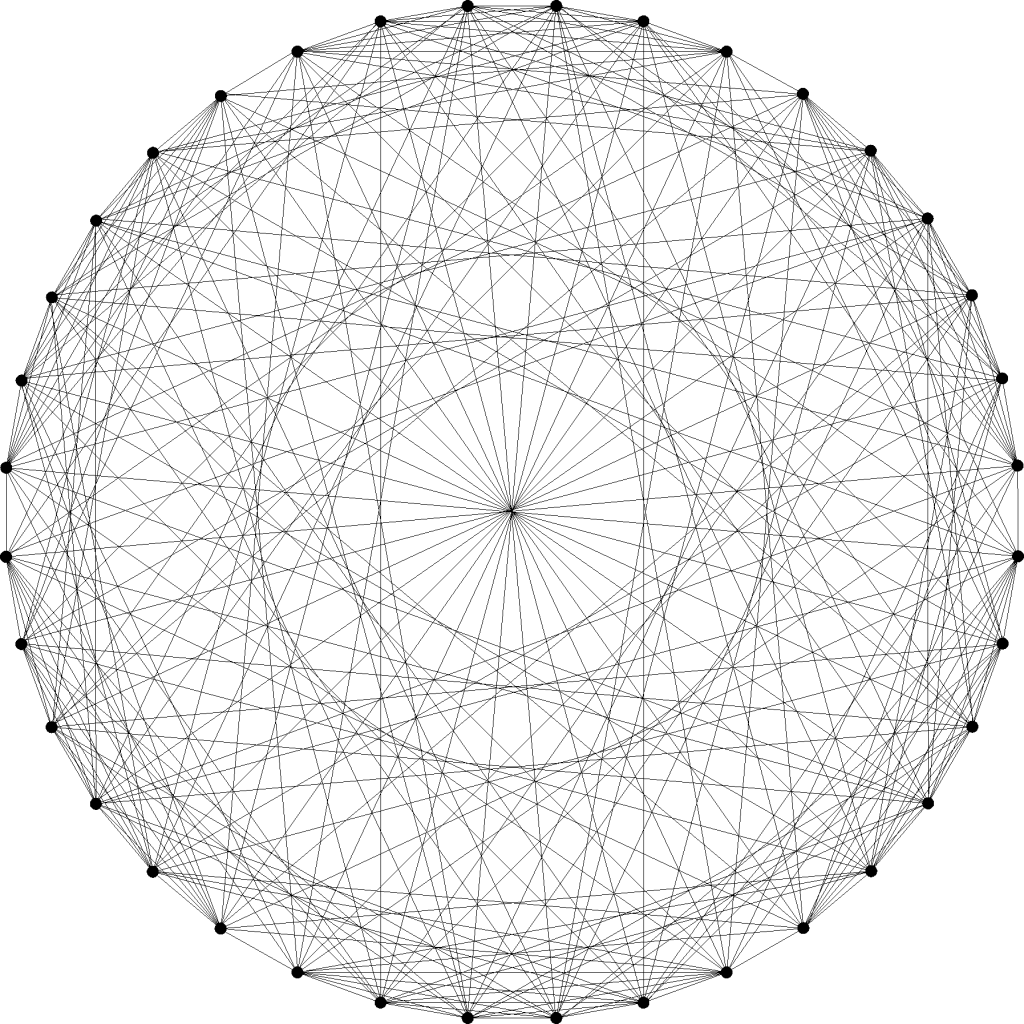
Hay quien se quedaría a gusto con esta solución (como nuestro flamante ganador). Pero quizás se debería cuestionar si de verdad puede existir un pueblo con 36 habitantes donde cada uno conozca a 15 vecinos, y cada pareja sea conocida exactamente por 6 personas. Los tiquismiquis que se lo hayan preguntado pueden ver el grafo de la figura, donde cada vértice representa a un vecino, y cada arista une a dos vecinos que se conocen. ¡Lo que me ha costado dibujarlo, oiga!

¿Que no se ve nada? Pues otra posible forma de verlo consiste en disponer a los 36 habitantes formando un cuadrado \(6\times 6\), desde la posición \((1,1)\) a la posición \((6,6)\), y considerar que el habitante \((i,j)\) conoce a todos los de su fila, a todos los de su columna, y a todos los de su diagonal (esto último quiere decir a todos los \((p,q)\) tales que \(i-j=p-q\) módulo 6).

Esperamos que les haya gustado. Se admiten peticiones para el próximo. ¿Cómo dicen? ¿Más fácil? Bueno, ya veremos…

En un pueblo con \(12 k\) habitantes, cada uno conoce a \(3k+6\) convecinos y el conocimiento es mutuo. Existe un entero positivo \(n\) tal que, para cada pareja de habitantes, el número de personas que conocen a ambos es \(n\). ¿Cuántos habitantes hay en el pueblo?

Esperamos las soluciones en blog.algebra@gmail.com

A continuación, la presentación de esta nueva sección y las instrucciones de uso… Continuar leyendo “Problemas tenemos tós (1): La red social.”

El siguiente juego ha sido patentado por Akio Kawauchi, Ayaka Shimizu, Kengo Kishimoto, de OCAMI (Osaka City University Advanced Mathematical Institute).

Se basa en el siguiente resultado de teoría de nudos: Tomemos el diagrama de un nudo (una representación plana, con los cruces señalando qué trozo de cuerda pasa por arriba y qué trozo por debajo). Habremos dividido el plano en distintas regiones. Supongamos que al elegir una región, cambiamos el sentido de todos los cruces que están en el borde de esa región. El teorema dice que, por muy complicado que sea el nudo, hay una forma de ir eligiendo regiones de modo que acabemos con el nudo trivial.

En el juego, los autores han cambiado “cruces” por “bombillas”. Comenzamos con algunas bombillas encendidas y otras apagadas. Se trata de ir eligiendo regiones de manera que terminemos con todas las bombillas encendidas.

Hagan juego…

Ya hay solución para el cuadragésimo y último de los desafíos matemáticos con los que EL PAÍS ha celebrado el centenario de la Real Sociedad Matemática Española. Recordemos que el reto que propuso Adolfo Quirós, profesor de la Universidad Autónoma de Madrid y coordinador desde la RSME de esta iniciativa, consistía en descifrar el siguiente mensaje secreto:

47175413325413337313226277154179412371521522771

La clave para descifrar el mensaje es pensar cómo podemos llegar a 9 símbolos (los números del 1 al 9) a partir de algo que utiliza los símbolos 0, 1 y 2, resultado de escribir en base 3. Resulta que si, en lugar de números de 3 cifras en base 3, consideramos números de 2 cifras en base 3, obtenemos los números del 0(=00 en base 3) al 8(=22 en base3). Esto no es exactamente lo que tenemos, pero casi: habría que sumar 1 para tener los números del 1 al 9.

Así, podíamos deducir que quizás lo que se haya hecho es agrupar las cifras en base 3 de dos en dos, escribir el correspondiente número en base 10 y sumar 1. Un paso previo a descifrar el mensaje podía ser comprobar si esto funciona en los ejemplos que se daban. Observemos que en el caso de PEDRO para agrupar de dos en dos nos falta una cifra, y añadimos un 0 al final (esta es la pequeña diferencia técnica entre número par o impar de letras).

Ejemplo 1: HOLA -> 7,15,11,0 -> 021120102000 -> 02 11 20 10 20 00 -> 246360 -> 357471

Ejemplo 2: PEDRO -> 16,4,3,18,15 -> 121011010200120 -> 12 10 11 01 02 00 12 00 -> 53412050 -> 64523161

¡Efectivamente funciona! Esto podría ser casualidad, pero no es probable, así que vamos a aplicarlo a nuestro desafío a ver qué obtenemos (no escribiremos explícitamente el paso de restar una unidad ni el de volver a agrupar los dígitos en base 3 que estaban separados de 2 en 2). Así:

4 7 1 7 5 4 1 3 3 2 5 4 1 3 3 3 7 3 1 3 2 2 6 2 7 7 1 5 4 1 7 9 4 1 2 3 7 1 5 2 1 5 2 2 7 7 1 -> 10 20 00 20 11 10 00 02 02 01 11 10 00 02 02 02 20 02 00 02 01 01 12 01 20 20 00 11 10 00 20 22 10 00 01 02 20 00 11 01 00 11 01 01 20 20 0 -> 11, 0, 19, 12, 0, 20, 4, 12, 0, 20, 8, 2, 0, 19, 4, 19, 20, 0, 13, 0, 20, 21, 0, 11, 18, 4, 3, 4, 3, 15, 18 -> LASMATEMATICASESTANATUALREDEDOR

Y, efectivamente, ‘Las matemáticas están a tu alrededor’ es el mensaje que, tras alguna vacilación en algún caso por errores de transcripción que han sido capaces de enmendar, han obtenido 993 de los 994 lectores que han enviado respuestas.

El cuadragésimo y último de los desafíos con los que hemos celebrado el centenario de la Real Sociedad Matemática Española lo presenta Adolfo Quirós, profesor de la Universidad Autónoma de Madrid y coordinador desde la RSME de esta iniciativa.

Enunciado: Queremos transmitir un mensaje secreto. Para eso vamos a transformar un texto, que está escrito en el alfabeto castellano de 27 letras, de la A a la Z (incluyendo Ñ y W), en otro texto que se escribe usando solo 9 símbolos: los números del 1 al 9. Veamos como lo hacemos y lo ilustraremos con dos ejemplos.

Primero numeramos las letras por orden del 0 al 26, A=0, B=1, C=2, D=3,…, N=13, Ñ=14,…, W=23, X=24, Y=25, Z=26. Por ejemplo:

HOLA-> 7,15,11,0

PEDRO->16,4,3,18,15

A continuación escribimos cada uno de esos números como un número de tres cifras en base 3. Recordemos lo que esto quiere decir: Los números los escribimos normalmente en base 10, usando unidades (1=10^0), decenas (10=10^1), centenas (100=10^2), etc. Así, 3418 representa el número 3×10^3+4×10^2+1×10+8. Para escribir en base 3 usamos potencias de 3, y sólo necesitamos las cifras 0, 1 y 2. Por ejemplo, la expresión 212 en base 3 representa la cantidad 2×3^3+1×3+2, que en base 10 se escribiría como 23.

Nuestras letras quedarán entonces representadas por A=000, B=001, C=002, D=010, …, N=111, Ñ= 112,…, W=212, X=220, Y=221, Z=222. Siguiendo con nuestros ejemplos:

HOLA-> 7,15,11,0 -> 021120102000

PEDRO->16,4,3,18,15 -> 121011010200120

Obsérvese que hemos escrito 3 cifras por cada número (no hemos quitado los ceros a la izquierda) y, también, que hemos escrito todos los números seguidos, sin las comas que los separaban antes. Ahora viene la parte secreta. Haciendo algo que no os vamos a decir, porque descubrirlo es precisamente el desafío, transformamos finalmente nuestros textos en otros escritos usando sólo los números del 1 al 9. En los ejemplos:

HOLA-> 7,15,11,0 -> 021120102000 -> 357471

PEDRO->16,4,3,18,15 -> 121011010200120 -> 64523161

El desafío consiste en leer el siguiente mensaje, que ha sido cifrado usando el procedimiento que hemos descrito, incluida la parte secreta:

47175413325413337313226277154179412371521522771

ALGUNAS OBSERVACIONES IMPORTANTES. En el texto original no se utilizan signos de puntuación, acentos, ni siquiera los espacios entre palabras, que serían otro símbolo. Una buena idea es ir probando los procedimientos que se os ocurran en los dos ejemplos. Estrictamente hablando, el procedimiento es ligeramente distinto si el texto original tiene un número par o impar de letras, pero la diferencia no influye en nada en cómo leer los mensajes, es una cuestión puramente técnica que resultará evidente a posteriori. Se considerará válida cualquier solución que haya sido capaz de descifrar el código y dé el mensaje correcto, pero, como siempre, nos gustaría saber cómo habéis llegado a ella.